Basic Plasma Science
Electron-Positron ("pair") Plasmas
“Pair” plasmas are of interest due to their unique plasma properties such as the absence of Faraday rotation and parametric decay, enhanced nonlinear Landau damping, and solitary-wave behavior. They are also important in astrophysical settings such as at the poles of neutron stars. They are predicted to have many novel properties. We are participating in an experiment to make the first studies of a simultaneously confined pair plasma.
We are participating in a collaboration (APEX) to confine and study a pair plasma at the intense positron beam (NEPOMUC) in Munich. The goal is to create pair plasma with densities ~ 1012 mi-3 and temperature ≤ 0.5 eV. First experiments will be done with bursts of 108 – 109 positrons from the specially designed trap and accumulator shown. A multicell trap for ≥ 1010 positrons is also being developed. Two (alternative) confinement devices are planned for these experiments, a levitated magnetic dipole and an optimized stellarator [Stoneking, J. Plasma Phys. (2020)].
Further Reading:
Laboratory electron-positron plasma-a new research object, V. Tsytovich and C. Wharton, Comm. Pl. Phys. Cont. Fusion 4, 91 (1978).
A new frontier in laboratory physics: magnetized electron–positron plasmas, M. Stoneking, et al., J. Plasma Phys. 86, 155860601 (2020)
Toward a compact levitated superconducting dipole for positron-electron plasma confinement, M. Stoneking, et al., Nonneutral Plasma Physics IX, (AIP Conf. Proc. 1928, 2018), p. 1.
Lossless Positron Injection into a Magnetic Dipole Trap, E. V. Stenson, et al., Phys. Rev. Lett. 121, 235005 (2018).
Plans for the creation and studies of electron–positron plasmas in a stellarator, T. S. Pedersen, New J. Phys. 14, 035010 (2012).
Confinement and manipulation of electron plasmas in a multicell trap, N. Hurst, et al., Phys. Plasmas 26, 013513 (2019).
Simultaneous confinement of low-energy electrons and positrons in a compact magnetic mirror trap, H. Higaki, et al., N. J. Phys. 19, 023016 (2017).
Practical limits on positron accumulation and the creation of electron-positron plasmas, R. G. Greaves, Non-Neutral Plasma Physics IV, F. Anderegg, et al., eds. (AIP, NY, 2002), p. 10.
A Multicell Trap to Confine Large Numbers of Positrons, C. M. Surko and R. G. Greaves, Radiation Physics and Chemistry 68, pp. 419-425 (2003).
Vortex Dynamics
Under certain conditions, magnetized electron plasmas obey a set of equations that are directly analogous to the equations governing 2D inviscid (ideal) fluid dynamics. This analogy allows us to study 2D vorticity dynamics offering distinct advantages over traditional fluid experiments such as water tanks. We are focusing on the case of vortices subjected to externally imposed E x B flows.
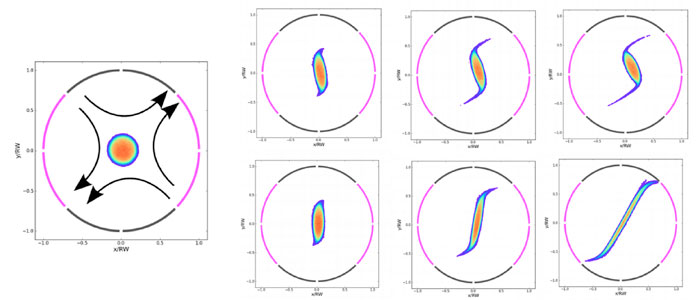
The experiments are conducted using the 8-Segment Trap (8ST) described in the Tools section. A segmented electrode is used to apply external ExB flows to the electron plasmas. The resulting dynamics are analogous to that of vortices subject to ambient flows. Recently, we have focused on vortices under applied strain flows.
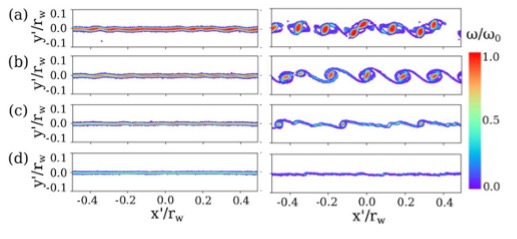
Rows (a) -> (d) show increasing strain rate applied to a vortex shear layer, and the left and right panels show the time evolution of the resulting Kelvin instability (the Kelvin-Helmholtz instability in a shear layer of finite thickness). Increasing the strain rate results in a delay, but not a complete suppression, of the instability.
The lower figure shows the evolution (left -> right) of a strained vortex with (e) a Gaussian vorticity profile and (f) a flat-top vorticity profile. The Gaussian vortex is destroyed by spatial Landau damping, whereas the flat-top vortex survives, albeit perturbed.
Further Reading:
Adiabatic behavior of an elliptical vortex in a time-dependent external strain flow, N. C. Hurst, J. R. Danielson, D. H. E. Dubin, and C. M. Surko, Phys. Rev. Fluids, 6, 054703 (2021).
Instability of an electron-plasma shear layer in an externally imposed strain flow, N. C. Hurst, J. R. Danielson, D. H. E. Dubin, and C. M. Surko, Phys. Plasmas 27, 042101 (2020)
Experimental study of the stability and dynamics of a two-dimensional ideal vortex under external strain, N. C. Hurst, J. R. Danielson, D. H. E. Dubin, and C. M. Surko, J. Fluid Mech. 848, 256 (2018).
Evolution of a Vortex in a Strain Flow, N. C. Hurst, J. R. Danielson, D. H. E. Dubin, and C. M. Surko, Phys. Rev. Lett. 117, 235001 (2016).
Bounce-Average Orbits
During operation of the Multi-Cell Test Structure (MCTS), we discovered an unexpected phenomenon: a plasma spanning two Penning-Malmberg cells with non-coinciding axes will execute a non-circular orbit dictated by the average of the diocotron drifts in each cell. These orbits are enabled by fast axial bounce motion across the two cells (so-called “bounce-average” dynamics).
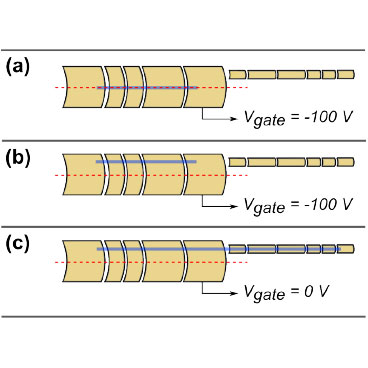
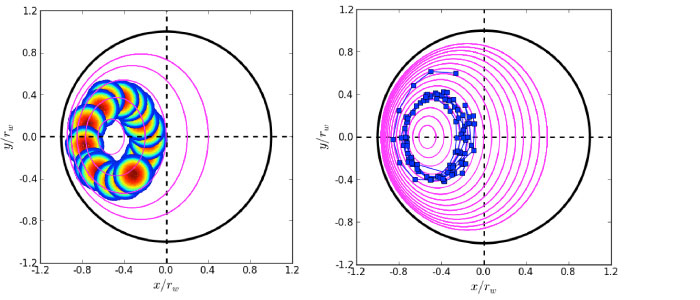
The bounce-average orbits (also referred to as “competing-drift orbits”) were discovered during the process of transferring plasma from the large-diameter master cell into one of 3 small-diameter off-axis storage cells. This process is shown in the figure to the right. In panel (a), we begin with a plasma (blue line) confined on the axis of the master cell. In panel (b), we use autoresonant diocotron excitation to move the plasma across the magnetic field to the location of the storage cell. Finally, in panel (c), we open the gate separating master and storage cell, allowing plasma to stream between the two cells. At this point, plasma particles bounce rapidly back and forth between the master and the storage cell.
Because plasma motion perpendicular to the magnetic field is relatively slow, the diocotron drift of the plasma is an average of the separate drifts in each cell. While the diocotron drift in a single cell traces out a circle aligned with the cell axis, the bounce-averaged diocotron drift traces out an approximately elliptical shape (shown above, within the boundary of the storage cell).
Further reading:
Confinement and manipulation of electron plasmas in a multicell trap, N. Hurst, J. Danielson, C. Baker, C. Surko, Phys. Plasmas 26, 013513 (2019).
Electron Plasma Orbits from Competing Diocotron Drifts, N. Hurst, J. Danielson, C. Baker, C. Surko, Phys. Rev. Lett. 113, 025004 (2014).
