Previous Projects

1. Home
2. Previous Projects
3. Convection

TRANSITION FROM CURVED TO ANGULAR TEXTURES

Convection in a binary mixture is characterized by traveling-wave convection, but if the Rayleigh number is increased above a certain threshhold, the propagation velocity goes to zero and stationary convection is observed. We have found that the stationary convection patterns observed in this regime are different from those observed in a pure liquid. Near the traveling-wave transition the patterns are angular, consisting of geometric domains of straight rolls, whereas at higher Rayleigh number, the texture of the pattern is curved.

For an account of the theoretical basis of convection textures, see "Ingredients of a Theory of Convective Textures Close to Onset", M. C. Cross, Physical Review A25, 1065 (1982).

The basic idea is that a stable convection pattern is one which maintains a wavenumber close to it's optimum value (roughly twice the height of the convection cell), and has a minimum of curvature. Straight rolls are obviously the best solution, but in a geometry in which straight rolls are not possible, (such as our cylindrical cell) a compromise is necessary. We beleive the angular and curved textures results from competition between wavenumber and curvature optimization.

OBSERVATIONS IN AN 8% ETHANOL MIXTURE

We first observed the transition in a mixture of 8% ethanol (by weight) in water. This mixture supports a strongly nonlinear, large amplitude traveling-wave convection state.

THE CURVED TEXTURE

This pattern was observed at reduced Rayleigh number 3.7.

THE ANGULAR TEXTURE

This pattern was observed at reduced Rayleigh number 1.7, just above the transition to traveling-wave convection.

LOCAL CURVATURE IN THE CURVEDTEXTURE

In this image, the curvature is evenly distributed along the roll boundaries. This is a favorable curvature distribution.

LOCAL CURVATURE IN THE ANGULARTEXTURE

In this image, the curvature is zero in most parts of the pattern, but very intense along the boudaries of the straight domains. This is an unfavorable curvature distribution.

LOCAL WAVENUMBER IN THE CURVEDTEXTURE

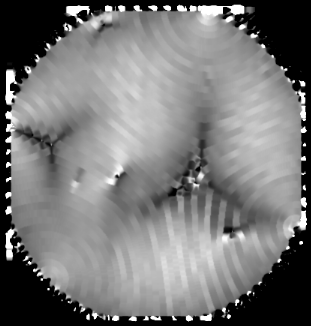
In this image, there is intense wavenumber frustration in the region near the defects where the domain boundaries meet. This is an unfavorable wavenumber distribution.

LOCAL WAVENUMBER IN THE ANGULARTEXTURE

In this image, the wavenumber is uniform and equal to the system's prefered wavenumber. This is a favorable wavenumber distribution.

ILLUSTRATION OF THETWO TEXTURES

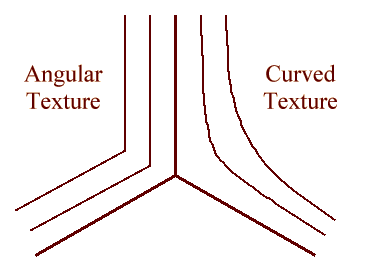
Our understanding of this transition is that the pattern wants to optimize both its wavenumber distribution (by having it uniform) and its curvature distribution (by having is uniform). The defects in the pattern make it impossible for both conditions to be fulfilled at once. Notice that in the sketch above, which illustrates the arrangement of rolls near a defect, the angular texture has sharp corners (bad for wavenumber), put perfect wavenumber, and the curved texture has better curvature (more smooth) but wavenumber distortion. We believe that the transition from a curved to angular texture is a crossover from optimization of wavenumber at the expense of curvature (angular texture), to optimization of curvature at the expense of wavenumber.

OBSERVATIONS IN AN 1% ETHANOL MIXTURE, AND IN PURE WATER

In a 1% ethanol mixture, the traveling-wave state is still observed, but it is of smaller amplitude, and occurs at lower Rayleigh number. In pure water, there is no traveling-wave state. We found that the angular texture could be observed in the 1% mixture, but that it did not occur in pure water, indicating that it is associated to the transition to traveling-waves.

CONVECTIONPATTTERN IN THE 1% MIXTURES

The two images show the convection pattern at Rayleigh number 1.7 and 1.3, respectively. Although the topology of the pattern is different than that observed with the 8% mixture, the transition to an angular state is clear.

CURVATURE IN THE1% MIXTURES

Here the curvature of the two patterns shown above is calculated. The lines of intense curvature in the left-hand picture indicate the angular texture.

CONVECTIONPATTERN IN THE PURE WATER

Here we try to repeat the experiment in pure water. In the mixture, the angular state forms as we lower the Rayleigh number and approach the traveling-wave state. In the pure fluid, there is not traveling-wave state, and the angular texture does not form as we lower the Rayleigh number and approach the onset value.

CURVATURE IN THE PURE WATER

The curvature maps confirm that the angular texture does not form in the pure fluid.

In this summary, we have tried to give an intuitive argument as to why the curved and angular textures are related to the competition between wavenumber and curvature frustration. In our paper (cited above) we introduce an effective free energy based on the Swift-Hohenberg model which seems to capture the essence of the transition.

We believe that the transition is of general interest, because it illustrates the difference between curved patterns, such are typically observed in Rayleigh-Benard convection, and angular patterns, such as are found in ferromagnetic garnets, for instance. (See Seul, et. al., Science 254, 1616 (1991)).

"Transition from curved to angular texture in binary fluid convection." A. La Porta, K. D. Eaton, and C. M. Surko, Phys. Rev. E53 570, (1996).