Annhiliation positrons
History and Iwata Plot
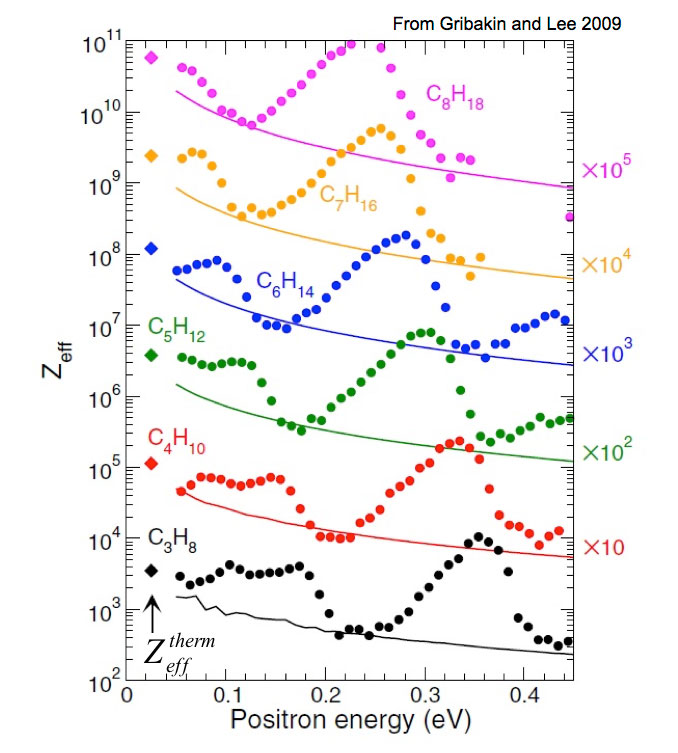
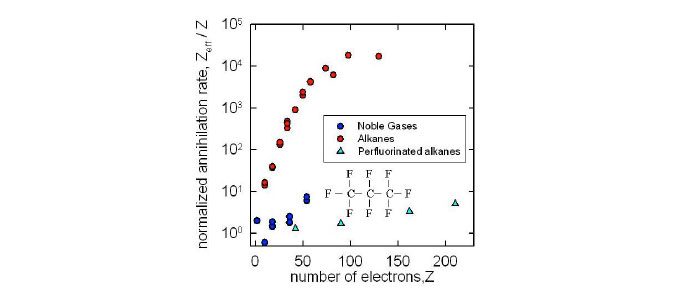
While positron annihilation on atoms and molecules has been studied since the 1940s, the BGT offered new opportunities to study in the trap interaction of a dilute test gas with a known positron distribution. Early studies confirmed molecular annihilation rates much larger than those expected for simple collisions, and many chemical trends (left) were established. Indirect evidence was interpreted as evidence for positron attachment as the origin of these large rates.
Further Reading
[1] For comprehensive annihilation experiments: K. Iwata, et al., Phys. Rev. A 51, 473 (1995).
[2] Early evidence of positron attachment: C. M. Surko, et. al., Phys. Rev. Lett. 61, 1831 (1988).
Annihilation-rate Energy Spectra
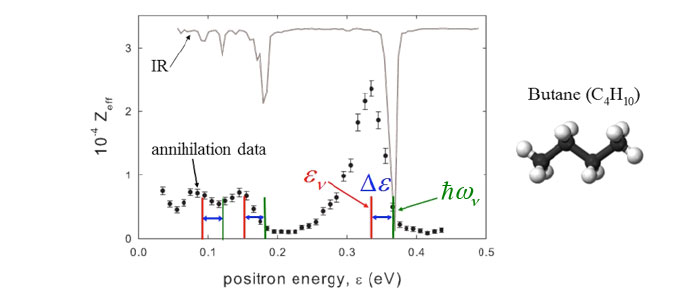
The use of the trap-based beam to measure annihilation rates on molecules as a function of positron energy led to the discovery of large resonances associated with the molecular vibrations (e.g., butane shown at the left). A key result of this and similar measurements is that these resonances provide evidence that molecules can bind positrons. Further, the observed energy shifts from the energies of the vibrations provide a measure of the positron binding energy. To date, similar spectra have been measured for over 75 molecules, providing evidence that positrons bind to all but the smallest molecules.
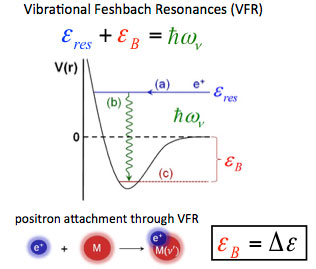
The explanation for these resonances (right) is that, if there is a positron bound state on the molecule, the incident positron can excite a vibrational Feshbach resonance when the incoming positron energy is εres = ℏω ν − εβ, where ℏω ν is the energy of a vibration and εβ is the positron-molecule binding energyν. Once in the bound state, the resulting increase in the overlap of the positron wave function with those of the molecular electrons results in a greatly enhanced annihilation rate. The positions of these resonances provide a measure of positron-molecule binding energies. The molecule can subsequently de-excite, ejecting the positron and thereby limiting the amplitude of the annihilation peak.
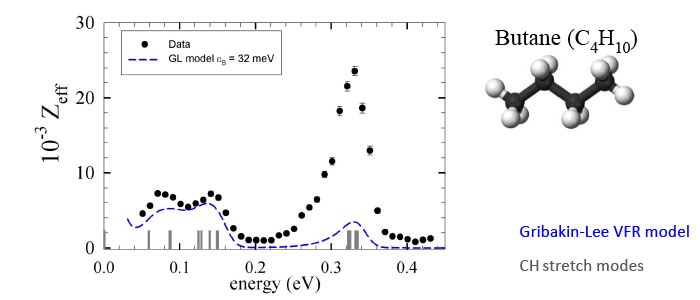
When only one vibrational mode is involved, a seminal theory by Gribakin and Lee is in quantitative agreement with the observed annihilation spectra. However, in general, vibrational mode coupling is operative [i.e., intramolecular vibrational energy transfer (IVR)]. In this case, the spectra are more complicated. Developing a quantitative theory of the resulting vibrational dynamics and annihilation spectra is the subject of ongoing research.
Further reading:
Positron-molecule interactions: Resonant attachment, annihilation, and bound states, G. Gribakin, J. Young, and C. Surko, Rev. Mod. Phys. 82, 2257 (2010).
Vibrational Feshbach Resonances Mediated by Nondipole Positron-Molecule Interactions, M. R. Natisin, et al., Phys. Rev. Lett. 119, 113402 (2017).
Enhanced resonant positron annihilation due to non-fundamental modes in molecules, S. Ghosh, et al., Phys. Rev. Lett. 125, 173401 (2020).
Positron annihilation in molecules by capture into vibrational Feshbach resonances of infrared-active modes, G. Gribakin and C. Lee, Phys. Rev. Lett., 93, 193201 (2006).
Vibrational resonance enhancement of positron annihilation in molecules, S. J. Gilbert, et al., Phys. Rev. Lett. 88, 043201 (2002).
Mode-coupling Effects and IVR
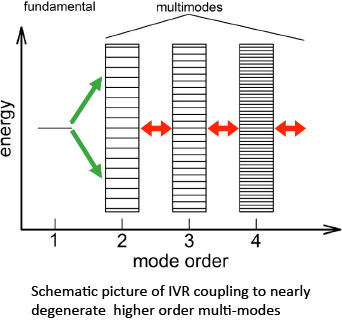
Although the Gribakin-Lee model of VFR provides a qualitative picture of resonant positron annihilation on molecules, vibrational mode coupling (not considered in the simple theory) typically results in additional effects. This mode-coupling process is often referred to as “intramolecular vibrational redistribution,” or IVR in the chemistry literature. Depending upon the coupling of the positron bound state to the positron continuum via de-excitation of the coupled modes, the lifetime of the resonance can either be increased or decreased, leading respectively to either enhancement or suppression of the annihilation rate.
In a molecule, the normal modes (fundamentals) are typically not independent vibrations. Instead, they can be coupled through anharmonic terms. This results in the IVR process in which the molecular vibrational energy is redistributed into multimode vibrational excitations.
A schematic diagram of this process is shown to the right. The coupling strength decreases with increasing mode order and increasing energy separation; and so, typically, only nearly degenerate modes are important. While simple models of this process have been proposed, the development of a quantitative theory of resonant positron annihilation when multimode effects are important is the subject of ongoing research.
Further reading:
Mode coupling and multiquantum vibrational excitations in Feshbach-resonant positron annihilation in molecules, G. F. Gribakin, J. F. Stanton, et al., Phys. Rev. A. 96, 062709 (2017).
Modeling enhancement and suppression of vibrational Feshbach resonances in positron annihilation on molecules, J. Danielson et al., Phys. Rev. A 88, 062702 (2013).
Positron-molecule interactions: Resonant attachment, annihilation, and bound states, G. Gribakin, J.Young, and C. Surko, Rev. Mod. Phys. 82, 2257 (2010).
Positron annihilation in large polyatomic molecules: The role of vibrational Feshbach resonances and binding, G Gribakin and C. Lee, Eur. Phys. J. D. 51, 51 (2009).
Role of Combination Vibrations in Resonant Positron Annihilation, J. A. Young, G. F. Gribakin, C. M. R. Lee, and C. M. Surko, Phys. Rev. A 77, 060702(R), pp. 1-4 (2008).
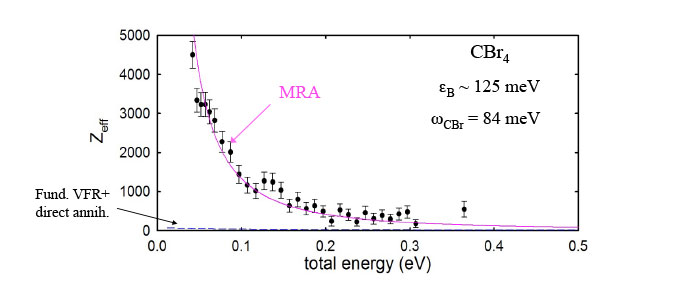
Multi-mode Resonances
The annihilation spectra of most molecules are dominated by the excitation of fundamental vibrations. However, even in this case overtone and combination mode features are observed. An extreme case as shown above in CBr4 occurs when the positron binding energy is so large that no fundamentals can be excited (i.e., εB > ℏω ν). Yet, even in this case, a relatively large annihilation rate is observed. A model of this has been proposed (“multi-mode resonant annihilation or MRA). Comparison with the data is shown as the solid line.
Particularly in large molecules, such MRA features are prominent in the space between the fundamentals. A fitof an MRA model to the spectra of larger alkane molecules is shown at the right. This effect has been used to explain the large annihilation rates observed for thermal positrons at 300 K interacting with various molecular species. These multi-modes are also likely the key to understanding the role of IVR in enhancing or suppressing the annihilation rates of the fundamental resonances.
Further reading:
Resonant Annihilation and Positron Bound States in Benzene, S. Ghosh, et al., Phys. Rev. Lett. 129, 123401 (2022).
Enhanced resonant positron annihilation due to non-fundamental modes in molecules, S. Ghosh, et al., Phys. Rev. Lett. 125, 173401 (2020).
Mode coupling and multi-quantum vibrational excitations in Feshbach-resonant positron annihilation in molecules, G. F. Gribakin, J. F. Stanton, et al., Phys. Rev. A. 96, 062709 (2017).
Ubiquitous Nature of Multimode Vibrational Resonances in Positron-Molecule Annihilation, A. Jones et al., Phys. Rev. Lett., 108, 093201 (2012).
Role of combination vibrations in resonant positron annihilation, J. Young et al., Phys. Rev. A 77, 060702(R) (2008).